We're going to skip over the finer details of the KeyExpansion phase for now. The main point is that it takes in our 16 byte key and produces 11 4x4 matrices called "round keys" derived from our initial key. These round keys allow AES to get extra mileage out of the single key that we provided.

The initial key addition phase, which is next, has a single AddRoundKey step. The AddRoundKey step is straightforward: it XORs the current state with the current round key.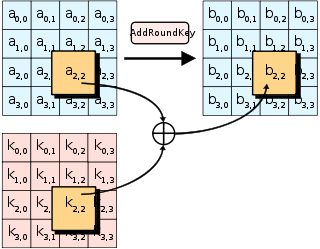



AddRoundKey also occurs as the final step of each round. AddRoundKey is what makes AES a "keyed permutation" rather than just a permutation. It's the only part of AES where the key is mixed into the state, but is crucial for determining the permutation that occurs.

As you've seen in previous challenges, XOR is an easily invertible operation if you know the key, but tough to undo if you don't. Now imagine trying to recover plaintext which has been XOR'd with 11 different keys, and heavily jumbled between each XOR operation with a series of substitution and transposition ciphers. That's kinda what AES does! And we'll see just how effective the jumbling is in the next few challenges.

Complete the add_round_key function, then use the matrix2bytes function to get your next flag.

Challenge files:
  - add_round_key.py

You have solved this challenge! View solutions

You must be logged in to submit your flag.